스택 & 큐 with Javascript

스택(Stack)

스택은 마지막에 삽입된 항목만 제거할 수 있는 자료구조이다. 그래서 후입선출, Last In First Out(LIFO) 방식의 자료구조라고 일컬어진다.

 

스택

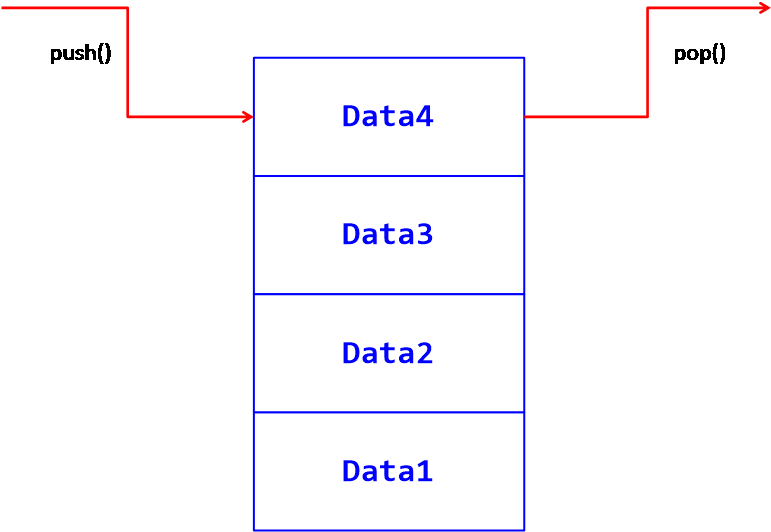
그리고 자바스크립트 배열은 이러한 스택의 특성을 그대로 살린 push()와 pop() 메소드를 제공한다. 따라서 자바스크립트 배열을 이용하면 손쉽게 스택을 구현할 수 있다.

 

생성

class Stack{
    constructor(arr){
        this.arr = []
        if(arr) this.arr = arr
    }
}

우선 Stack 클래스 내부에 멤버 변수로 배열을 하나 넣어준다.

삽입

push(val){
        this.arr.push(val)
}

그리고 배열의 push() 메소드를 이용하여 스택의 push()를 구현한다.

삭제

pop(){
        return this.arr.pop()
}

마찬가지로 pop()을 정의할 수 있다. 이때 pop()은 push()와 다르게 제거한 값을 반환한다는 점에 유의하자.

접근

top(){
        return this.arr[this.arr.length-1]
}

스택의 개념에 맞게 top()메소드는 가장 마지막에 삽입된 요소를 반환하도록 구현해준다. 여기까지하면 스택이라 불리기에 손색이 없다.

---

그런데 자료구조로서 의미를 더하려면 조금 더 자유롭게 접근하고 검색할 수 있어햐 한다. 따라서 위에서부터 n번째 요소에 접근하는 메소드와 특정 요소의 존재 여부를 검색하는 메소드를 생각해 볼 수 있다.

복사

copy(){
        return this.arr.slice()
}

접근과 검색을 할 때에 원본 배열을 건드리면 곤란하므로 copy() 메소드를 만들어준다.

n번째 요소 접근

function getStackNthTop(stack, n){
    if(n <=0) throw 'error'

    var copy = new Stack(stack.copy())
    while(--n != 0) copy.pop()
        
    return copy.pop()
}

간단하다. pop()을 n번 수행하면 n번째 요소에 접근할 수 있다. pop()의 시간복잡도는 O(1)이므로 n번째 요소에 접근하는 시간복잡도는 O(n)이다.

검색

function search(stack, element){
    var copy = new Stack(stack.copy())

    while(!copy.isEmpty()){
        if(element == copy.pop()) return true
    }

    return false
}

일종의 완전 탐색이다. 전체 요소를 돌면서 pop()을 수행하고 검색하려는 요소와 맞아떨어지면 true 반환한다. 역시 n개 요소를 돌기 때문에 시간복잡도는 O(n)이다.

---

전체 소스(테스트 코드)

class Stack{
    constructor(arr){
        this.arr = []
        if(arr) this.arr = arr
    }

    isEmpty(){
        return this.arr.length == 0
    }

    copy(){
        return this.arr.slice()
    }

    push(val){
        this.arr.push(val)
    }

    pop(){
        return this.arr.pop()
    }

    top(){
        return this.arr[this.arr.length-1]
    }
}

function getStackNthTop(stack, n){
    if(n <=0) throw 'error'

    var copy = new Stack(stack.copy())
    while(--n != 0) copy.pop()
        
    return copy.pop()
}

function search(stack, element){
    var copy = new Stack(stack.copy())

    while(!copy.isEmpty()){
        if(element == copy.pop()) return true
    }

    return false
}

function test(){
    var stack = new Stack()
    console.log(stack)
    //stack: empty
    
    for(var i=1; i<=5; i++)
        stack.push(i)
    console.log(stack)
    //stack: [1,2,3,4,5]

    stack.pop()
    console.log(stack)
    //stack: [1,2,3,4]

    console.log("top: " + stack.top())
    //top: 4

    console.log("2nd top: " + getStackNthTop(stack, 2))
    //2nd top: 3 

    console.log("seacrh 1: " + search(stack, 1)) //true
    console.log("seacrh 5: " + search(stack, 5)) //false
}

test()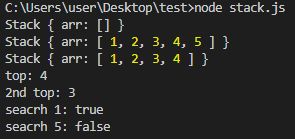

테스트 결과

---

큐(Queue)

큐는 스택과 반대로 가장 먼저 삽입된 항목만 제거할 수 있는 자료구조이다. 따라서 선입선출, First In First Out(FIFO) 방식의 자료구조라고 일컬어진다.

큐

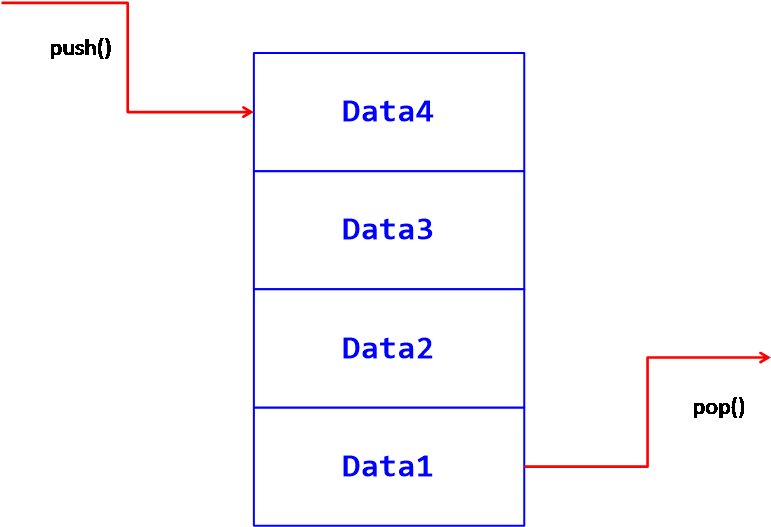
자바스크립트 배열은 큐의 특성을 살린 shift() 메소드 역시 포함하고 있다. 따라서 앞선 스택의 구현과 거의 비슷한 느낌으로 진행할 수 있다. 실제로 스택의 pop(), top()을 큐에서는 dequeue(), front()로서 다른 방향에서 접근할 뿐이다.

 

생성

class Queue{
    constructor(arr){
        this.arr = []
        if(arr) this.arr = arr
    }
}

삽입

enqueue(val){
        this.arr.push(val)
}

삭제

dequeue(){
        return this.arr.shift()
}

Javascript Array의 shift() 메소드에는 0번째 인덱스를 제거와 더불어 나머지 요소들의 인덱스 변경까지 포함되어 있다. 따라서 배열을 이용한 큐에서 요소 삭제의 시간복잡도는 O(n)이다.

접근

front(){
        return this.arr[0]
}

n번째 요소 접근

function getQueueNthFront(queue, n){
    if(n <=0) throw 'error'

    var copy = new Queue(queue.copy())
    while(--n != 0) copy.dequeue()

    return copy.dequeue()
}

검색

function search(queue, element){
    var copy = new Queue(queue.copy())

    while(!copy.isEmpty()){
        if(element == copy.dequeue()) return true
    }

    return false
}

---

전체 소스(테스트 코드)

class Queue{
    constructor(arr){
        this.arr = []
        if(arr) this.arr = arr
    }

    isEmpty(){
        return this.arr.length == 0
    }

    copy(){
        return this.arr.slice()
    }

    enqueue(val){
        this.arr.push(val)
    }

    dequeue(){
        return this.arr.shift()
    }

    front(){
        return this.arr[0]
    }
}

function getQueueNthFront(queue, n){
    if(n <=0) throw 'error'

    var copy = new Queue(queue.copy())
    while(--n != 0) copy.dequeue()

    return copy.dequeue()
}

function search(queue, element){
    var copy = new Queue(queue.copy())

    while(!copy.isEmpty()){
        if(element == copy.dequeue()) return true
    }

    return false
}

function test(){
    var queue = new Queue([1,2,3,4,5])
    console.log(queue) //queue: [1,2,3,4,5]

    queue.dequeue() 
    console.log(queue) //queue: [2,3,4,5]

    queue.enqueue(6) 
    console.log(queue) //queue: [2,3,4,5,6]
    
    console.log("2nd front: " + getQueueNthFront(queue, 2)) //2nd front: 3
    console.log("search 2: " + search(queue, 2)) //true
    console.log("search 7: " + search(queue, 7)) //false
}

test()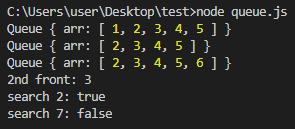

테스트 결과

---

정리

기본적으로 스택과 큐 모두 삽입, 삭제, 접근을 O(1)시간에 수행할 수 있다. 다만 위에서는 인덱스를 갖는 배열을 이용해서 큐의 dequeue() 메소드를 구현했기 때문에 이 경우의 시간복잡도는 O(n)이었다. 인덱스가 없는 연결 리스트(Linked List)를 이용해서 큐를 구현할 경우 O(1) 시간만에 가능하다. 또한 스택과 큐 모두 n번째 요소 접근과 검색을 O(n) 시간에 수행할 수 있다.

 

시간복잡도	삽입	삭제	접근	n번째 접근	검색
스택	O(1)	O(1)	O(1)	O(n)	O(n)
큐	O(1)	O(n) *	O(1)	O(n)	O(n)